Alexandar May's Blog
0%

Binary Tree

Posted on In
Symbols count in article: 7.4k Reading time ≈ 7 mins.

Binary Tree

  1. What is a Binary Tree?
  2. Key Components and Terms
  3. Types of Binary Tree On the basis of the completion of levels
  4. Tree Traversal Techniques
  5. Binary Search Tree (BST)
  6. Maximum Depth of Binary Tree
  7. Real-World Applications

1. What is a Binary Tree?

A binary tree is a tree data structure in which each node has at most two children, referred to as the left child and the right child.The topmost node is the root, and nodes without children are called leaves.It is commonly used in computer science for efficient storage and retrieval of data, with various operations such as insertion, deletion, and traversal.

1
2
3
4
5
     A  <- Root
   /   \
  B     C  <- Children
 / \
D   E  <- Leave

Generic TreeNode class:

1
2
3
4
5
6
7
8
9
10
11
12
13
public class TreeNode<T> where T : IComparable<T>
{
    public T Data { get; set; }
    public TreeNode<T>? Left { get; set; }
    public TreeNode<T>? Right { get; set; }

    public TreeNode(T data)
    {
        Data = data;
        Left = null;
        Right = null;
    }
}

2. Key Components and Terms:

  • Root: Top node (A in our example)
  • Parent/Child: A is parent of B and C
  • Leaf: Nodes without children (D, E, C)
  • Subtree: Any node with its descendants
  • Depth: Distance from the root to a node (root has default depth 1)
  • Height: Longest path from a node to a leaf
  • Level: All nodes at the same depth

3. Types of Binary Tree On the basis of the completion of levels

  • Complete Binary Tree
  • Perfect Binary Tree
  • Balanced Binary Tree

Perfect Binary Tree

A Binary tree is a Perfect Binary Tree in which all the internal nodes have two children and all leaf nodes are at the same level.
A Perfect Binary Tree of height h (where the height of the binary tree is the number of edges in the longest path from the root node to any leaf node in the tree, height of root node is 0) has $2^{h+1} - 1$ node.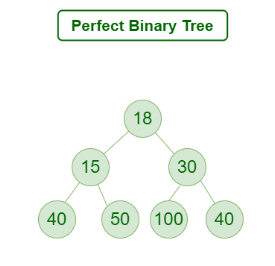
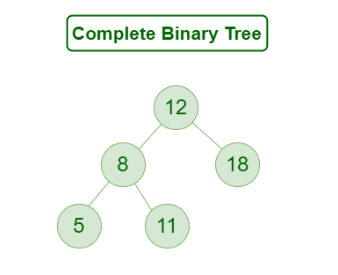
pic

Complete Binary Tree

A Binary Tree is a Complete Binary Tree if all the levels are completely filled except possibly the last level and the last level has all keys as left as possible.
A complete binary tree is just like a full binary tree, but with two major differences:

  • Every level except the last level must be completely filled.
  • All the leaf elements must lean towards the left.(I think they must be continuous from left to right)
  • The last leaf element might not have a right sibling i.e. a complete binary tree doesn’t have to be a full binary tree.
    pic

Full Binary Tree

A full binary tree is a binary tree with either zero or two child nodes for each node.
pic

Balanced Binary Tree

A binary tree is balanced if the height of the tree is O(Log n) where n is the number of nodes. For Example, the AVL tree maintains O(Log n) height by making sure that the difference between the heights of the left and right subtrees is at most 1(key attribute!). Red-Black trees maintain O(Log n) height by making sure that the number of Black nodes on every root to leaf paths is the same and that there are no adjacent red nodes. Balanced Binary Search trees are performance-wise good as they provide O(log n) time for search, insert and delete.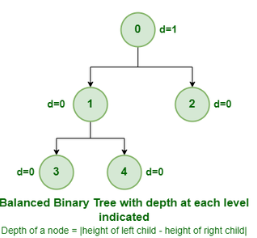
pic

4. Tree Traversal Techniques

Tree Traversal refers to the process of visiting or accessing each node of the tree exactly once in a certain order. Tree traversal algorithms help us visit and process all the nodes of the tree. Since a tree is not a linear data structure, there can be multiple choices for the next node to be visited. Hence we have many ways to traverse a tree.

  • Depth First Search or DFS
    • Inorder Traversal
    • Preorder Traversal
    • Postorder Traversal
  • Level Order Traversal or Breadth First Search or BFS

Depth-First Search (DFS)

  • Inorder Traversal (Left-Root-Right)

    1
    2
    3
    4
    5
    6
    void Inorder(TreeNode node) {
        if (node == null) return;
        Inorder(node.Left);
        Console.Write(node.Value + " ");
        Inorder(node.Right);
    }

    Output: D B E A C

  • Preorder Traversal (Root-Left-Right)

    1
    2
    3
    4
    5
    6
    void Preorder(TreeNode node) {
        if (node == null) return;
        Console.Write(node.Value + " ");
        Preorder(node.Left);
        Preorder(node.Right);
    }

    Output:A B D E C

  • Postorder Traversal (Left-Right-Root)

    1
    2
    3
    4
    5
    6
    void Postorder(TreeNode node) {
        if (node == null) return;
        Postorder(node.Left);
        Postorder(node.Right);
        Console.Write(node.Value + " ");
    }

    Output: D E B C A

Level Order Traversal or Breadth First Search or BFS 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public IList<IList<int>> LevelOrder(TreeNode root)
{
    var res = new List<IList<int>>();
    var que = new Queue<TreeNode>();
    if (root == null) return res;
    que.Enqueue(root);
    while (que.Count != 0)
    {
        var size = que.Count;
        var vec = new List<int>();
        for (int i = 0; i < size; i++)
        {
            var cur = que.Dequeue();
            vec.Add(cur.val);
            if (cur.left != null) que.Enqueue(cur.left);
            if (cur.right != null) que.Enqueue(cur.right);
        }
        res.Add(vec);
    }
    return res;
}

Output: A B C D E

5. Binary Search Tree (BST)

Accdoring to the wikipedia:

In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node’s left subtree and less than the ones in its right subtree. The time complexity of operations on the binary search tree is linear with respect to the height of the tree.

Time complexity in big O notation

Operation Average Worst case
Search O(log n) O(n)
Insert O(log n) O(n)
Delete O(log n) O(n)

BST Implementation 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class BinarySearchTree<T> where T : IComparable<T>
{
    private TreeNode<T>? _root;

    public void Insert(T data)
    {
        _root = InsertRec(_root, data);
    }

    private TreeNode<T> InsertRec(TreeNode<T>? node, T data)
    {
        if (node == null) return new TreeNode<T>(data);
        
        int comparison = data.CompareTo(node.Data);
        if (comparison < 0)
            node.Left = InsertRec(node.Left, data);
        else if (comparison > 0)
            node.Right = InsertRec(node.Right, data);
            
        return node;
    }

    public bool Search(T data)
    {
        return SearchRec(_root, data);
    }

    private bool SearchRec(TreeNode<T>? node, T data)
    {
        if (node == null) return false;
        
        int comparison = data.CompareTo(node.Data);
        return comparison == 0 || 
               SearchRec(comparison < 0 ? node.Left : node.Right, data);
    }
}

How to delete Node in a BST? 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public TreeNode DeleteNode(TreeNode root, int key)
{
    /*
     * 1.Not found the target key 
     * 
     * 2. Found
     * 2.1 the left and right node is null which mean its a leaf node
     * 2.2 the left is null and  the right is not null
     * 2.3 the left is not null and  the right is null
     * 2.4 Both left and right node is not null
     * 
     */
    //not found
    if (root == null) return null;
    //Found
    if(root.val == key)
    {
        if (root.left == null && root.right == null) return null;
        if (root.left == null && root.right != null) return root.right;
        if (root.left != null && root.right == null) return root.left;
        if (root.left != null && root.right != null)
        {
            TreeNode leftode = root.right;
            while(leftode.left != null)
            {
                leftode = leftode.left;
            }
            leftode.left = root.left;
            return root.right;
        }
    }
    if (root.val > key) root.left = DeleteNode(root.left, key);
    if (root.val < key) root.right = DeleteNode(root.right, key);

    return root;
}

6. Maximum Depth of Binary Tree

Given a binary tree, the task is to find the maximum depth of the tree. The maximum depth or height of the tree is the number of edges in the tree from the root to the deepest node.

  • Approach 1: Using Recursion – O(n) Time and O(h) Space

    1
    2
    3
    4
    5
    6
    7
    8
    public int MaxDepth(TreeNode root) {
        if(root == null) return 0;

        int leftDepth = MaxDepth(root.left);
        int rightDepth = MaxDepth(root.right);

        return 1 + Math.Max(leftDepth, rightDepth);
    }

  • Approach 2: Level Order Traversal without using Null Delimiter – O(n) Time and O(n) Space

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    public int MaxDepth(TreeNode root)
    {
        int depth = 0;
        Queue<TreeNode> que = new();
        if (root == null) return depth;
        que.Enqueue(root);
        while (que.Count != 0)
        {
            int size = que.Count;
            depth++;
            for (int i = 0; i < size; i++)
            {
                var node = que.Dequeue();
                if (node.left != null) que.Enqueue(node.left);
                if (node.right != null) que.Enqueue(node.right);
            }
        }
        return depth;
    }

7. Real-World Applications

  1. LINQ Query Optimization
    • Expression trees power LINQ queries
  2. Game Development
    • Unity uses spatial partitioning trees (Octrees/BVH)
  3. Database Systems
    • SQL Server uses B-trees for index storage